莫比乌斯指环

莫比乌斯带,又译梅比斯环或麦比乌斯带,是一种拓扑学结构,它只有一个面(表面),和一个边界。它是由德国数学家、天文学家莫比乌斯和约翰·李斯丁在1858年独立发现的。这个结构可以用一个纸带旋转半圈再把两端粘上之后轻而易举地制作出来。事实上有两种不同的莫比乌斯带镜像,他们相互对称。如果把纸带顺时针旋转再粘贴,就会形成一个右手性的莫比乌斯带,反之亦类似。

莫比乌斯带本身具有很多奇妙的性质。如果你从中间剪开一个莫比乌斯带,不会得到两个窄的带子,而是会形成一个把纸带的端头扭转了两次再结合的环(并不是莫比乌斯带),再把刚刚做出那个把纸带的端头扭转了两次再结合的环从中间剪开,则变成两个环。如果你把带子的宽度分为三分,并沿着分割线剪开的话,会得到两个环,一个是窄一些的莫比乌斯带,另一个则是一个旋转了两次再结合的环。

另外一个有趣的特性是将纸带旋转多次再粘贴末端而产生的。比如旋转三个半圈的带子再剪开后会形成一个三叶结。剪开带子之后再进行旋转,然后重新粘贴则会变成数个Paradromic。莫比乌斯带常被认为是无穷大符号「∞」的创意来源,因为如果某个人站在一个巨大的莫比乌斯带的表面上沿着他能看到的“路”一直走下去,他就永远不会停下来。但是这是一个不真实的传闻,因为「∞」的发明比莫比乌斯带还要早。
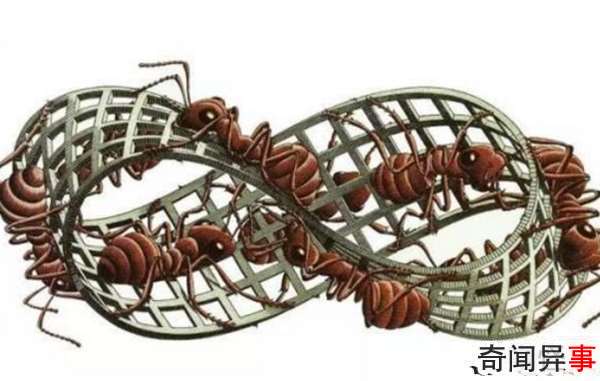
莫比乌斯环的诅咒
莫比乌斯环的形成很简单,把一条纸两头反过来接上,不管你从哪一个点出发,绕了半圈似乎已经绕出去,但再继续绕半圈后,又会发现回到原点。通俗点,我们就叫它死循环模式。莫比乌斯之环,就是无限循环的一个象征。这种莫比乌斯指环在现实生活中带给我们的是无尽的黑暗与恐惧。
有人说,莫比乌斯环是个诅咒之环,因为,一旦一个信念系统建立起来之后,你将永远无限循环的在这个信念里游走,除非你懂得解除莫比乌斯环的信念诅咒,否则你将永远循环在此诅咒中…当环境没有办法给我们选择的机会时,唯一的选择就是出去闯。当你觉得人生陷入了希望和错觉的循环,甚至是绝望时,你要做的是给自己一个机会破除诅咒、为自己的生活模式换血。

有好多电影情节都把莫比乌斯指环的诅咒作为剧情需要,以下的电影就是典型的受到莫比乌斯指环的诅咒的。
1、《恐怖游轮》

恐怖游轮,也是一部很出名的闭路循环式电影了。杰西,单身妈妈,周末跟好友共同出海游玩,结果遭遇风暴,登上了一艘名为“艾俄洛斯”的游轮,杰西在这游轮上发现了一件奇怪的事情,为了救回自己的儿子,陷入了万劫不复的恐怖轮回之中。
2、《环形使者》

“你好,30年后的自己”,乔的职业是名杀手,受雇于一家环形使者的杀手组织,他的任务就是杀死组织从未来送回来的人,可在一场任务中发现,自己要杀死的居然是未来的自己,而造成这一切的原因就是自己与未来自己的战斗,是自己造就了组织的老大“唤雨师”,乔如何才能走出这个死循环?
3、《前目的地》

改编自《你们这些还魂尸》,看完此片异灵君也没有懂,直到把简析看完之后,才发现作者脑洞大的吓人,如果你是烧脑电影爱好者,此部片子值得一看。
该片剧情前前后后都是由一个人完成,借助时光机,一次一次的深入死循环当中,就想简介中所说“我”逐渐发现了隐藏在时间悖论下不为人知的秘密,我们如同莫比乌斯环,周而复始的延续着我们的命运。
莫比乌斯环象征什么?

象征着循环往复、永恒、无限的。因此常被用于各类标志设计。
三个奇妙之处:
一、莫比乌斯环只存在一个面。

二、如果沿着莫比乌斯环的中间剪开,将会形成一个比原来的莫比乌斯环空间大一倍的、把纸带的端头扭转了四次再结合的环(并不是莫比乌斯带,在本文中将之编号为:环0),而不是形成两个莫比乌斯环或两个其它形式的环。

三、如果再沿着环0的中间剪开,将会形成两个与环0空间一样的、具有正反两个面的环,且这两个环是相互套在一起的,从此以后再沿着环1和环2以及因沿着环1和环2中间剪开所生成的所有环的中间剪开,都将会形成两个与环0空间一样的、具有正反两个面的环,永无止境。且所生成的所有的环都将套在一起,永远无法分开、永远也不可能与其它的环不发生联系而独立存在。

怎样理解莫比乌斯环?
公元1858年德学家莫比乌斯(Mobius,1790~1868)和约翰·李斯丁发现:把一根纸转180°后,两头再粘来做成的纸带圈,具有魔术般的性质。
普通纸带具有两个面(即双侧曲面),一个正面,一个反面,两个面可以涂成不同的颜色;而这样的纸带只有一个面(即单侧曲面),一只小虫可以爬遍整个曲面而不必跨过它的边缘。这种纸带被称为“莫比乌斯带”(也就是说,它的曲面只有一个)。
莫比乌斯带还有更为奇异的特性。一些在平面上无法解决的问题,却不可思议地在莫比乌斯带上获得了解决。
比如在普通空间无法实现的"手套易位"问题:人左右两手的手套虽然极为相像,但却有着本质的不同。我们不可能把左手的手套贴切地戴到右手上去;也不能把右手的手套贴切地戴到左手上来。无论你怎么扭来转去,左手套永远是左手套,右手套也永远是右手套!不过,倘若你把它搬到莫比乌斯带上来,那么解决起来就易如反掌了。
在自然界有许多物体也类似于手套那样,它们本身具备完全相像的对称部分,但一个是左手系的,另一个是右手系的,它们之间有着极大的不同。
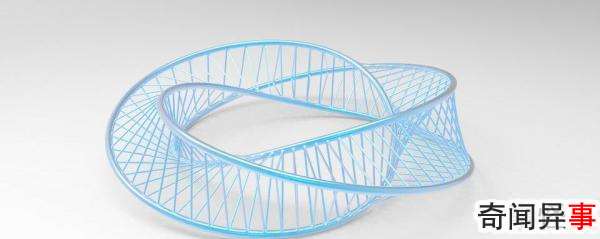
莫比乌斯带是一种拓展图形,它们在图形被弯曲、拉大、缩小或任意的变形下保持不变,只要在变形过程中不使原来不同的点重合为同一个点,又不产生新点。换句话说,这种变换的条件是:在原来图形的点与变换了图形的点之间存在着一一对应的关系,并且邻近的点还是邻近的点。这样的变换叫做拓扑变换。拓扑有一个形象说法——橡皮几何学。
因为如果图形都是用橡皮做成的,就能把许多图形进行拓扑变换。例如一个橡皮圈能变形成一个圆圈或一个方圈。但是一个橡皮圈不能由拓扑变换成为一个阿拉伯数字8。因为不把圈上的两个点重合在一起,圈就不会变成8,“莫比乌斯带”正好满足了上述要求。




