知识点:《四边形的定义》 收集:荆换粟 编辑:茉莉花仙子
本知识点包括:1、什么叫做四边形? 2、四边形的概念 3、初中数学中的平行四边形法则定义 4、什么条件可以证明四边形是平行四边形 5、哪些物体的表面是四边形? 。
《四边形的定义》相关知识
48定理 四边形的内角和等于360°
49四边形的外角和等于360°
50多边形内角和定理 n边形的内角的和等于(n-2)×180°
51推论 任意多边的外角和等于360°
52平行四边形性质定理1 平行四边形的对角相等
53平行四边形性质定理2 平行四边形的对边相等
54推论 夹在两条平行线间的平行线段相等
55平行四边形性质定理3 平行四边形的对角线互相平分
56平行四边形判定定理1 两组对角分别相等的四边形是平行四边形
57平行四边形判定定理2 两组对边分别相等的四边形是平行四边形
58平行四边形判定定理3 对角线互相平分的四边形是平行四边形
59平行四边形判定定理4 一组对边平行相等的四边形是平行四边形
60矩形性质定理1 矩形的四个角都是直角
61矩形性质定理2 矩形的对角线相等
62矩形判定定理1 有三个角是直角的四边形是矩形
63矩形判定定理2 对角线相等的平行四边形是矩形
64菱形性质定理1 菱形的四条边都相等
65菱形性质定理2 菱形的对角线互相垂直,并且每一条对角线平分一组对角
66菱形面积=对角线乘积的一半,即S=(a×b)÷2
67菱形判定定理1 四边都相等的四边形是菱形
68菱形判定定理2 对角线互相垂直的平行四边形是菱形
69正方形性质定理1 正方形的四个角都是直角,四条边都相等
70正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角
71定理1 关于中心对称的两个图形是全等的
72定理2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分
73逆定理 如果两个图形的对应点连线都经过某一点,并且被这一 点平分,那么这两个图形关于这一点对称
74等腰梯形性质定理 等腰梯形在同一底上的两个角相等
75等腰梯形的两条对角线相等
76等腰梯形判定定理 在同一底上的两个角相等的梯形是等腰梯形
77对角线相等的梯形是等腰梯形
78平行线等分线段定理 如果一组平行线在一条直线上截得的线段
相等,那么在其他直线上截得的线段也相等
79 推论1 经过梯形一腰的中点与底平行的直线,必平分另一腰
80 推论2 经过三角形一边的中点与另一边平行的直线,必平分第 三边
81 三角形中位线定理 三角形的中位线平行于第三边,并且等于它 的一半
82 梯形中位线定理 梯形的中位线平行于两底,并且等于两底和的 一半 L=(a+b)÷2 S=L×h
参考思路:
四边形是由四条线段围成的平面图形
知识拓展:
1:所有四边形的定义
知识要点归纳:
四条不重合的直线首尾依次相连构成的图形.
2:【四边形的定义】
知识要点归纳:
广义的是指由不在同一直线上四条线段依次首尾相接围成的封闭的图形,包括平面的和立体的.
狭义的只是指平面上由不在同一直线上四条线段依次首尾相接围成的封闭图形.
3:各种特殊四边形的判定定义如平行四边形,矩形,正方形,菱形等.
知识要点归纳:
平行四边形定义
(1)如果一个四边形是平行四边形,那么这个四边形的一组对边平行且相等.
(简述为“平行四边形的对边平行且相等”)
(2)如果一个四边形是平行四边形,那么这个四边形的两组对边分别平行.
(简述为“平行四边形的对边平行”)
(3)如果一个四边形是平行四边形,那么这个四边形的两组对边分别相等.
(简述为“平行四边形的对边相等”)
(4)如果一个四边形是平行四边形,那么这个四边形的两组对角分别相等.
(简述为“平行四边形的对角相等”)
(5)如果一个四边形是平行四边形,那么这个四边形的两条对角线互相平分.
(简述为“平行四边形的两条对角线互相平分”)
(6)平行四边形是中心对称图形,对称中心是两条对角线的交点.
(7)一般的平行四边形不是轴对称图形.
平行四边形判定
(1)两组对边分别相等的四边形是平行四边形.
(2)对角线互相平分的四边形是平行四边形.
(3)一组对边平行且相等的四边形是平行四边形.
(4)两组对边分别平行的四边形是平行四边形.
(5)两组对角分别相等的四边形是平行四边形.(不可直接证明为平行四边形)
矩形(rectangle)是一种平面图形,矩形的四个角都是直角,同时矩形的对角线相等,而且矩形所在平面内任一点到其两对角线端点的距离的平方和相等.
判定
( 1)对角线相等的四边形是矩形;( ×) (2)对角线互相平分且相等的四边形是矩形;(√)
(3)有一个角是直角的四边形是矩形;(×)
(4)有四个角是直角的四边形是矩形;(√)
(5)四个角都相等的四边形是矩形S;(√)
(6)对角线相等,且有一个角是直角的四边形是矩形;(×)
(7)一组邻边垂直,一组对边平行且相等的四边形是矩形;(√)
(8)对角线相等且互相垂直的四边形是矩形.(×)
说明:
(l)所给四边形添加的条件不满足三个的肯定不是矩形;
(2)所给四边形添加的条件是三个独立条件,但若与定理不同,则需要利用定义和判定定理证明或举反例,才能下结论.
正方形定义
同一平面内四条相同长度线段首尾顺次连接围成的封闭四边形.
四条边都相等且一个角是直角的四边形叫做正方形.
有一组邻边相等的矩形是正方形.
有一组邻边相等且一个角是直角的平行四边形是正方形.
有一个角为直角的菱形是正方形.
对角线平分,垂直且相等,并且交角为直角的四边形为正方形.
正方形判定方法
1:对角线相等的菱形是正方形.
2:对角线互相垂直的矩形是正方形,.对角线互相垂直,平分且相等的四边形是正方形.正方形是一种特殊的矩形.
3:四边相等,有三个角是直角的四边形是正方形.
4:一组邻边相等的矩形是正方形.
5:一组邻边相等且有一个角是直角的平行四边形是正方形.
6:四边均相等,对角线互相垂直平分且相等的四边形是正方形.
7:有一个角为直角的菱形是正方形.
8:依次连接四边形各边中点所得的四边形称为中点四边形.不管原四边形的形状怎样改变,中点四边形的形状始终是平行四边形.正方形的中点四边形是正方形.
9:既是菱形又是矩形的四边形是正方形.
菱形定义
一组邻边相等的平行四边形是菱形(rhombus)
四边相等的四边形是菱形(rhombus)
菱形判定
一组邻边相等的平行四边形是菱形
四边相等的四边形是菱形
关于两条对角线都成轴对称的四边形是菱形
对角线互相垂直且平分的四边形是菱形.
依次连接四边形各边中点所得的四边形称为中点四边形.不管原四边形的形状怎样改变,中点四边形的形状始终是平行四边形.菱形的中点四边形是矩形(对角线相等的四边形的中点四边形定为矩形) ,对角线互相垂直的四边形的中点四边形定为菱形.
菱形是在平行四边形的前提下定义的,首先它是平行四边形,但它是特殊的平行四边形,特殊之处就是“有一组邻边相等”,因而就增加了一些特殊的性质和不同于平行四边形的判定方法.
4:我们知道:有两条边相等的三角形叫做等腰三角形.类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形.(1)请写出一个你学过的特殊四边形中是等对边四边形的图形的名
知识要点归纳:
 (1)如:平行四边形、等腰梯形等.
(1)如:平行四边形、等腰梯形等.
(2)答:与∠A相等的角是∠BOD(或∠COE),
∵∠BOD=∠OBC+∠OCB=30°+30°=60°,
∴∠A=∠BOD,
猜想:四边形DBCE是等对边四边形;
(3)答:此时存在等对边四边形,是四边形DBCE.
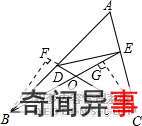
证法一:如图,作CG⊥BE于G点,作BF⊥CD交CD延长线于F点.
∵∠DCB=∠EBC=1 2
∴△BCF≌△CBG,
∴BF=CG,
∵∠BDF=∠ABE+∠EBC+∠DCB,∠BEC=∠ABE+∠A,
∴∠BDF=∠BEC,
∴△BDF≌△CEG,
∴BD=CE
∴四边形DBCE是等对边四边形.
证法二:如图,以C为顶点作∠FCB=∠DBC,CF交BE于F点.
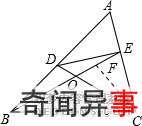
∵∠DCB=∠EBC=
| 1 |
| 2 |
∴在△BDC与△CFB中,
|
∴△BDC≌△CFB(ASA),
∴BD=CF,∠BDC=∠CFB,
∴∠ADC=∠CFE,
∵∠ADC=∠DCB+∠EBC+∠ABE,∠FEC=∠A+∠ABE,
∴∠ADC=∠FEC,
∴∠FEC=∠CFE,
∴CF=CE,
∴BD=CE,
∴四边形DBCE是等对边四边形.
说明:当AB=AC时,BD=CE仍成立.
5:【特殊四边形的性质,判定和定义】
知识要点归纳:
去百科看看吧
猜你喜欢:
1:什么叫做四边形?
提示:由不在同一直线上的不交叉的四条线段按照既定的顺序首尾相接,最后围成一个封闭的平面或立体图形,这个图形就叫做四边形。四边形一共有四条边,可根据四条边的长度、特性等分为不同的四边形,连接四边形任意两个不相邻顶点的线段为对角线,每个...
2:四边形的概念
提示:1,四边形由不在同一直线上四条线段依次首尾相接围成的封闭的平面图形或立体图形叫四边形,由凸四边形和凹四边形组成。 2,长方形 长方形(又称矩形)定义为四个内角相等的四边形,即是说所有内角均为直角。从这个定义可以得出矩形两条相对的边...
3:初中数学中的平行四边形法则定义
提示:平行四边形的定义:在同一平面内有两组对边分别平行的四边形叫做平行四边形. 平行四边形的定义、性质: (1)平行四边形对边平行且相等. (2)平行四边形两条对角线互相平分.(菱形和正方形) (3)平行四边形的对角相等,两邻角互补 (4)连接任...
4:什么条件可以证明四边形是平行四边形
提示:平行四边形的判定条件: 1、两组对边分别平行的四边形是平行四边形(定义判定法); 2、一组对边平行且相等的四边形是平行四边形; 3、两组对边分别相等的四边形是平行四边形; 4、两组对角分别相等的四边形是平行四边形(两组对边平行判定); ...
5:哪些物体的表面是四边形?
提示:表面是四边形的物体太多了。 房子桌子书本鞋盒墨水盒粉笔盒火柴盒窗户电脑屏幕黑板砖头毛巾等等 四边形定义 四边形由不在同一直线上的不交叉的四条线段依次首尾相接围成的封闭的平面图形或立体图形叫四边形。 凸四边形 四个顶点在同一平面内,对...


