知识点:《初中数学知识点大全》 收集:苏滞偌 编辑:月季姐姐
本知识点包括:1、初中数学知识点归纳 2、初中数学知识有哪些? 3、初中数学知识点整理 4、初中数学知识有哪些?简单概括 5、初三数学知识点 。
《初中数学知识点大全》相关知识
初中数学知识点总结
一、基本知识
一、数与代数A、数与式:1、有理数有理数:①整数→正整数/0/负整数②分数→正分数/负分数
数轴:①画一条水平直线,在直线上取一点表示0(原点),选取某一长度作为单位长度,规定直线上向右的方向为正方向,就得到数轴.②任何一个有理数都可以用数轴上的一个点来表示.③如果两个数只有符号不同,那么我们称其中一个数为另外一个数的相反数,也称这两个数互为相反数.在数轴上,表示互为相反数的两个点,位于原点的两侧,并且与原点距离相等.④数轴上两个点表示的数,右边的总比左边的大.正数大于0,负数小于0,正数大于负数.
绝对值:①在数轴上,一个数所对应的点与原点的距离叫做该数的绝对值.②正数的绝对值是他的本身、负数的绝对值是他的相反数、0的绝对值是0.两个负数比较大小,绝对值大的反而小.
有理数的运算:加法:①同号相加,取相同的符号,把绝对值相加.②异号相加,绝对值相等时和为0;绝对值不等时,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值.③一个数与0相加不变.
减法:减去一个数,等于加上这个数的相反数.
乘法:①两数相乘,同号得正,异号得负,绝对值相乘.②任何数与0相乘得0.③乘积为1的两个有理数互为倒数.
除法:①除以一个数等于乘以一个数的倒数.②0不能作除数.
乘方:求N个相同因数A的积的运算叫做乘方,乘方的结果叫幂,A叫底数,N叫次数.
混合顺序:先算乘法,再算乘除,最后算加减,有括号要先算括号里的.
2、实数 无理数:无限不循环小数叫无理数
平方根:①如果一个正数X的平方等于A,那么这个正数X就叫做A的算术平方根.②如果一个数X的平方等于A,那么这个数X就叫做A的平方根.③一个正数有2个平方根/0的平方根为0/负数没有平方根.④求一个数A的平方根运算,叫做开平方,其中A叫做被开方数.
立方根:①如果一个数X的立方等于A,那么这个数X就叫做A的立方根.②正数的立方根是正数、0的立方根是0、负数的立方根是负数.③求一个数A的立方根的运算叫开立方,其中A叫做被开方数.
实数:①实数分有理数和无理数.②在实数范围内,相反数,倒数,绝对值的意义和有理数范围内的相反数,倒数,绝对值的意义完全一样.③每一个实数都可以在数轴上的一个点来表示.
3、代数式
代数式:单独一个数或者一个字母也是代数式.
合并同类项:①所含字母相同,并且相同字母的指数也相同的项,叫做同类项.②把同类项合并成一项就叫做合并同类项.③在合并同类项时,我们把同类项的系数相加,字母和字母的指数不变.
4、整式与分式
整式:①数与字母的乘积的代数式叫单项式,几个单项式的和叫多项式,单项式和多项式统称整式.②一个单项式中,所有字母的指数和叫做这个单项式的次数.③一个多项式中,次数最高的项的次数叫做这个多项式的次数.
整式运算:加减运算时,如果遇到括号先去括号,再合并同类项.
幂的运算:AM+AN=A(M+N)
(AM)N=AMN
(A/B)N=AN/BN 除法一样.
整式的乘法:①单项式与单项式相乘,把他们的系数,相同字母的幂分别相乘,其余字母连同他的指数不变,作为积的因式.②单项式与多项式相乘,就是根据分配律用单项式去乘多项式的每一项,再把所得的积相加.③多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加.
公式两条:平方差公式/完全平方公式
整式的除法:①单项式相除,把系数,同底数幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连同他的指数一起作为商的一个因式.②多项式除以单项式,先把这个多项式的每一项分别除以单项式,再把所得的商相加.
分解因式:把一个多项式化成几个整式的积的形式,这种变化叫做把这个多项式分解因式.
方法:提公因式法、运用公式法、分组分解法、十字相乘法.
分式:①整式A除以整式B,如果除式B中含有分母,那么这个就是分式,对于任何一个分式,分母不为0.②分式的分子与分母同乘以或除以同一个不等于0的整式,分式的值不变.
分式的运算:
乘法:把分子相乘的积作为积的分子,把分母相乘的积作为积的分母.
除法:除以一个分式等于乘以这个分式的倒数.
加减法:①同分母分式相加减,分母不变,把分子相加减.②异分母的分式先通分,化为同分母的分式,再加减.
分式方程:①分母中含有未知数的方程叫分式方程.②使方程的分母为0的解称为原方程的增根.
B、方程与不等式
1、方程与方程组
一元一次方程:①在一个方程中,只含有一个未知数,并且未知数的指数是1,这样的方程叫一元一次方程.②等式两边同时加上或减去或乘以或除以(不为0)一个代数式,所得结果仍是等式.
解一元一次方程的步骤:去分母,移项,合并同类项,未知数系数化为1.
二元一次方程:含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程.
二元一次方程组:两个二元一次方程组成的方程组叫做二元一次方程组.
适合一个二元一次方程的一组未知数的值,叫做这个二元一次方程的一个解.
二元一次方程组中各个方程的公共解,叫做这个二元一次方程的解.
解二元一次方程组的方法:代入消元法/加减消元法.
一元二次方程:只有一个未知数,并且未知数的项的最高系数为2的方程
1)一元二次方程的二次函数的关系
大家已经学过二次函数(即抛物线)了,对他也有很深的了解,好像解法,在图象中表示等等,其实一元二次方程也可以用二次函数来表示,其实一元二次方程也是二次函数的一个特殊情况,就是当Y的0的时候就构成了一元二次方程了.那如果在平面直角坐标系中表示出来,一元二次方程就是二次函数中,图象与X轴的交点.也就是该方程的解了
2)一元二次方程的解法
大家知道,二次函数有顶点式(-b/2a,4ac-b2/4a),这大家要记住,很重要,因为在上面已经说过了,一元二次方程也是二次函数的一部分,所以他也有自己的一个解法,利用他可以求出所有的一元一次方程的解
(1)配方法
利用配方,使方程变为完全平方公式,在用直接开平方法去求出解
(2)分解因式法
提取公因式,套用公式法,和十字相乘法.在解一元二次方程的时候也一样,利用这点,把方程化为几个乘积的形式去解
(3)公式法
这方法也可以是在解一元二次方程的万能方法了,方程的根X1={-b+√[b2-4ac)]}/2a,X2={-b-√[b2-4ac)]}/2a
3)解一元二次方程的步骤:
(1)配方法的步骤:
先把常数项移到方程的右边,再把二次项的系数化为1,再同时加上1次项的系数的一半的平方,最后配成完全平方公式
(2)分解因式法的步骤:
把方程右边化为0,然后看看是否能用提取公因式,公式法(这里指的是分解因式中的公式法)或十字相乘,如果可以,就可以化为乘积的形式
(3)公式法
就把一元二次方程的各系数分别代入,这里二次项的系数为a,一次项的系数为b,常数项的系数为c
4)韦达定理
利用韦达定理去了解,韦达定理就是在一元二次方程中,二根之和=-b/a,二根之积=c/a
也可以表示为x1+x2=-b/a,x1x2=c/a.利用韦达定理,可以求出一元二次方程中的各系数,在题目中很常用
5)一元一次方程根的情况
利用根的判别式去了解,根的判别式可在书面上可以写为“△”,读作“diao ta”,而△=b2-4ac,这里可以分为3种情况:
I当△>0时,一元二次方程有2个不相等的实数根;
II当△=0时,一元二次方程有2个相同的实数根;
III当△B,A+C>B+C
在不等式中,如果减去同一个数(或加上一个负数),不等式符号不改向;例如:A>B,A-C>B-C
在不等式中,如果乘以同一个正数,不等号不改向;例如:A>B,A*C>B*C(C>0)
在不等式中,如果乘以同一个负数,不等号改向;例如:A>B,A*C
知识拓展:
1:正四边形的外接圆半径,用a表示.正五边形的外接圆半径,用a表示.正六边形的外接圆半径,用a表示.n边形的外接圆半径,用a表示.
知识要点归纳:
a为n边形的边长,四边形外接圆半径:√2a/2,五边形:a/2cos54°,六边形:a
n变形:a/(2cos((n-2)90°/n))画出图形,用三角函数余弦就可以
2:【怎么提高初中数学基础知识?】
知识要点归纳:
我认识到数学概念是数学定理,公式的依据,学生如果对数学概念弄不清,那么数学运算、推理就会无法进行下去.所以教学数学概念是教好数学课的重要一环.而要弄清数学概念,不但要从正面去讲,还要从反面,侧面去弄清它.例如:初二平面几何讲“平行线”概念时,教师以黑板相对两边为例,它们都是在同一平面内,若把它们看作是线段,则无论怎样延长也不会相交,这样就把平行线定义归纳为:“同一平面内”,“不相交的两条直线.”为了讲清“同一平面内”,教师再以反面问学生:教室中挂吊扇的铁管(垂直于地面的)与黑板的边线也不会相交,但是不是平行线呢?学生回答:不是平行线,因为它们不在同一平面内.从而突出了,必须是同一平面内,而且要不相交.我认为这样从正、反两方面讲清概念,学生印象较深刻.
二、查漏补缺,弥补学生的知识缺陷.
我意识到学生起点较低,知识缺陷大,如不及时给学生弥补知识缺陷,将会失去学习信心,学不下去.我的做法是:
1、初中一年级,对新生进行摸底测验,了解学生在小学学过的数学知识,哪些掌握较差.
2、结合新课,弥补学生的知识缺陷.例如,学习有理数运算时,结合与学生补分数通分,分数四测运算的知识.学习平面几何的相似形时,与学生补有关比例的知识.
3、对一些基础较差的学生,利用课余时间与之补课.
4、在作业中或测验中发现学生的知识缺陷,不轻易放过,要及时给学生指出,并要求学生重做.
三、充分运用启发式教学法,激发学生学习数学的积极性,提高自学数学的能力.
在教学课中,是采用启发式教学法还是注入式教学法是大不相同.采用启发式,能使学生积极主动地获取知识,充分调动学生的学习积极性和主动性.
怎么启发学生的积极思维呢?我认为,要结合教学内容恰当地提出问题,引导学生去积极思考寻求正确的答案.教师可以提出问题,让学生去思考、回答,也可以教师自问自答.但要防止提出的问题过于简单,学生只回答“是”或“不是”,这是达不到启发思维目的的.例如:初二平面几何讲“三角形内角和定理”关键是启发学生过三角形的某个顶点作对边的平行线,提出:要证明三个内角和等于180o,有什么办法呢?我们学过什么角等于180o的?(学生回答:平角).因此就要想办法把这三角形的三个内角拼成一个平角,学生自然就会想起作平行线了.
我还注意在课堂上培养学生自学教学书的能力,指导学生在课前或堂上阅读课文.同时编印适量的课外练习题,鼓励学生在课外主动多做一些练习题,使学生学得积极主动.
四、精讲多练,加强课堂练习,提高运算能力.
我在讲课中,尽量做到抓住关键问题精讲,留出一定时间让学生课堂练习;有时则讲练结合,边讲边练.对于例题,我也不是全部讲,有些例题可以在堂上通过学生练习后再讲.这样,学生动手练习后,教师再归纳小结,指出学生练习中出现的错误,印象较深刻,也及时纯正了学生易犯的错误.
五、交代解题规律,教给学生思考问题的方法.
我认为:在讲例题时,一定要交代解题规律,交给学生解题的锁匙.
例如:列方程解应用题是数学教学的一个难点,我在教列方程解应用题时,反复告诉学生:要抓住量与量的相等关系来列等式.对于行程问题,主要是利用距离、速度、时间三者关系.根据题意,利用距离的相等关系或时间的相等关系来列出等式.
又如,讲二元二次方程组解法时,告诉学生:主要是消元或降次.可想办法运用加、减法消去一个未知数(消元)或想办法消去二次项,或分解成一次因式的乘积(降次),如果是缺一次项的,可以想法消去常数项,变为二次齐次式来分解因式.
其他教学内容,也各有各的规律,教师必须告诉学生,让学生掌握解题规律.
六、认真批改学生作业,发现问题及时评讲,纠正作业中普遍性错误.
虽然批改作业是一件十分费时的事情,要花费不少精力,但我考虑到学生基础较差,作业错误较多,为了对学生知识质量负责,花一定时间去批改学生的作业还是必要的,因此,我做到全批全改学生作业,在批改中发现问题及时评讲.同时还采用一些有效措施来督促学生依时缴交作业,对不交作业的学生及时教育.
3:【现在有本书,有初一到三年级的基础和概念但是我不知道怎么理解,怎么运用他.请大家们指指招.那本书就叫做中考宝典记载着一到三年级的基础请家教我也想但是,我平时请教的那些同】
知识要点归纳:
这是在给大家出难题吧?
唉,还是事在人为吧!只要肯努力,什么时候都不晚,哪怕你现在高三,都不是问题,前提是你没有在正确的时间内做正确的事情(当然你可能由于其他原因造成这种局面),现在就要比常人付出更多;如果不努力,即便你现在初一,又有何用?
附:只要你想学,不用管别人怎么说,自己尽管做就是了,自己的路自己走.
好比马拉松,现在无非比别人晚了三年,这又怎么样啊?!路长着呢!
4:【如图,在平面直角坐标系中,已知一圆弧过小正方形网格的格点A、B、C,已知A点的坐标是(-3,5),则该圆弧所在圆的圆心坐标是______.】
知识要点归纳:
圆弧所在圆的圆心是AB与BC的垂直平分线的交点.
AB的垂直平分线是x=-1,点B的坐标是(1,5),C的坐标是(4,2),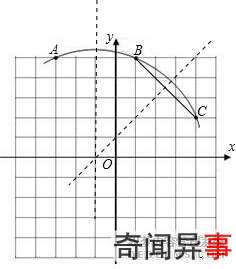
BC的垂直平分线与x=-1的交点的纵坐标是0,
因而该圆弧所在圆的圆心坐标是(-1,0).
猜你喜欢:
1:初中数学知识点归纳
提示:初中数学知识点大全 1、一元一次方程根的情况 △=b2-4ac 当△>0时,一元二次方程有2个不相等的实数根; 当△=0时,一元二次方程有2个相同的实数根; 当△
2:初中数学知识有哪些?
提示:初中数学知识点总结 一、基本知识 一、数与代数A、数与式:1、有理数有理数:①整数→正整数/0/负整数②分数→正分数/负分数 数轴:①画一条水平直线,在直线上取一点表示0(原点),选取某一长度作为单位长度,规定直线上向右的方向为正方向,就得到...
3:初中数学知识点整理
提示:复习核心注重课本知识,查漏补缺注重课堂学习,提高效率注意知识的迁移,学会融会贯通试卷的基本情况1.试卷结构:由填空、选择、解答题等28个题目组成。2.考试内容:根据《数学课程标准》要求,将对“数与代数”“空间与图形”“统计与概率”“实践与综...
4:初中数学知识有哪些?简单概括
提示:知识点1:一元二次方程的基本概念 知识点2:直角坐标系与点的位置 知识点3:已知自变量的值求函数值 1.当x=2时,函数y=的值为1. 2.当x=3时,函数y=的值为1. 3.当x=-1时,函数y=的值为1. 知识点4:基本函数的概念及性质 1.函数y=-8x是一次函数. 2.函...
5:初三数学知识点
提示:初三数学知识点 第一章二次根式 1 二次根式:形如 ( )的式子为二次根式; 性质: ( )是一个非负数; ; 。 2 二次根式的乘除: ; 。 3 二次根式的加减:二次根式加减时,先将二次根式华为最简二次根式,再将被开方数相同的二次根式进行合并。...


