知识点：《勾股定理练习题》 收集：詹呛脖 编辑：梅花姐姐
本知识点包括：1、初二数学勾股定理难一点的应用题，要有答案。谢谢。 2、勾股定理练习题 3、谁能帮我出一道关于勾股定理的题？ 4、勾股定理很难的题？（最好有答案）谢谢了，大神帮忙啊 5、我需要最最最基础的勾股定理题 。
《勾股定理练习题》相关知识
勾股定理测试题
一、选择题（每小题4分,共40分）
1、下列各组数中,能构成直角三角形的是（ ）
A：4,5,6 B：1,1, C：6,8,11 D：5,12,23
2、在Rt△ABC中,∠C＝90°,a＝12,b＝16,则c的长为（ ）
A：26 B：18 C：20 D：21
3、在平面直角坐标系中,已知点P的坐标是(3,4),则OP的长为（ ）
A：3 B：4 C：5 D：
4、在Rt△ABC中,∠C＝90°,∠B＝45°,c＝10,则a的长为（ ）
A：5 B： C： D：
5、下列定理中,没有逆定理的是（ ）
A：两直线平行,内错角相等 B：直角三角形两锐角互余
C：对顶角相等 D：同位角相等,两直线平行
6、△ABC中,∠A、∠B、∠C的对边分别是a、b、c,AB＝8,BC＝15,CA＝17,则下列结论不正确的是（ ）
A：△ABC是直角三角形,且AC为斜边 B：△ABC是直角三角形,且∠ABC＝90°
C：△ABC的面积是60 D：△ABC是直角三角形,且∠A＝60°
7、等边三角形的边长为2,则该三角形的面积为（ ）
A： B： C： D：3
8、已知a、b、c是三角形的三边长,如果满足 ,则三角形的形状是（ ）
A：底与边不相等的等腰三角形 B：等边三角形
C：钝角三角形 D：直角三角形
9、如图一艘轮船以16海里∕小时的速度从港口A出发向东北方向航行,另一轮船12海里∕小时从港口A出发向东南方向航行,离开港口3小时后,则两船相距（ ）
A：36 海里 B：48 海里 C：60海里 D：84海里
10、若 中, ,高AD=12,则BC的长为（ ）
A：14 B：4 C：14或4 D：以上都不对
二、填空题（每小题4分,共40分）
11、木工师傅要做一个长方形桌面,做好后量得长为80cm,宽为60cm,对角线为100cm,则这个桌面 （填“合格”或“不合格”）；
12、如图所示,以 的三边向 外作正方形,其面积分别
为 ,且 ；
13、将长为10米的梯子斜靠在墙上,若梯子的上端到梯子的底端的
距离为6米,则梯子的底端到墙的底端的距离为 ；
14、如图, ,则AD= ；
15、若三角形的三边满足 ,则这个三角形中最大的角为 ；
16、已知一个直角三角形的两条直角边分别为6cm、8cm,那么这个直角三角形斜边上的高为 ；
17、写出一组全是偶数的勾股数是 ；
18、如图,是一个三级台阶,它的每一级的长、宽、高分别为
20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是 ；
19、如图,已知一根长8m的竹杆在离地3m处断裂,竹杆顶部抵着地
面,此时,顶部距底部有 m；
20、一艘小船早晨8：00出发,它以8海里/时的速度向东航行,1小时后,另一艘小船以12海里/时的速度向南航行,上午10：00,两小相距 海里.
三、解答题（每小题10分,共70分）
21、如图,为修通铁路凿通隧道AC,量出∠A=40°∠B＝50°,AB＝5公里,BC＝4公里,若每天凿隧道0.3公里,问几天才能把隧道AB凿通?
22、如图,每个小方格的边长都为1．求图中格点四边形ABCD的面积.
23、如图所示,有一条小路穿过长方形的草地ABCD,若AB=60m,BC=84m,AE=100m,则这条小路的面积是多少?
24、如图,已知在△ABC中,CD⊥AB于D,AC＝20,BC＝15,DB＝9.
25、如图9,在海上观察所A,我边防海警发现正北6km的B处有一可疑船只正在向东方向8km的C处行驶.我边防海警即刻派船前往C处拦截.若可疑船只的行驶速度为40km/h,则我边防海警船的速度为多少时,才能恰好在C处将可疑船只截住?
26、如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm．当小红折叠时,顶点D落在BC边上的点F处（折痕为AE）．想一想,此时EC有多长?
知识拓展：
1：【初二勾股定理练习题直角三角形的一直角边长为12,另外两边之长为自然数,则满足要求的直角三角形共有（）A、4个B、5个C、6个D、8个】
知识要点归纳：
（a,b,c）叫做勾股数组,整数a,b,c满足a^2＋b^2＝c^2这个条件
由a^2＋b^2＝c^2及a,b,c互质可知,a,b必是一奇一偶,c必是奇.不妨设a为奇,则方程化为b^2＝（c＋a）（c－a）,由c,a互质可知,a－c和a＋c互质,从而方程可以化为（b/2）^2＝（c＋a）/2×（c－a）/2,令（c＋a）/2＝m^2,（c－a）/2＝n^2 （m,n互质）,即可解出,a＝m^2－n^2,b＝2mn,c＝m^2＋n^2（m,n互质,从而一奇一偶）,此即本原勾股数组公式
下面是100以内的勾股数,其中一直角边为12的有4个（故答案选A）：
i＝3 j＝4 k＝5
i＝5 ●【j＝12】 k＝13 …………………………………………①
i＝6 j＝8 k＝10
i＝7 j＝24 k＝25
i＝8 j＝15 k＝17
i＝9 ●【j＝12】 k＝15 …………………………………………②
i＝9 j＝40 k＝41
i＝10 j＝24 k＝26
i＝11 j＝60 k＝61
●【i＝12】＝12 j＝16 k＝20 …………………………………………③
●【i＝12】 j＝35 k＝37 …………………………………………④
i＝13 j＝84 k＝85
i＝14 j＝48 k＝50
i＝15 j＝20 k＝25
i＝15 j＝36 k＝39
i＝16 j＝30 k＝34
i＝16 j＝63 k＝65
i＝18 j＝24 k＝30
i＝18 j＝80 k＝82
i＝20 j＝21 k＝29
i＝20 j＝48 k＝52
i＝21 j＝28 k＝35
i＝21 j＝72 k＝75
i＝24 j＝32 k＝40
i＝24 j＝45 k＝51
i＝24 j＝70 k＝74
i＝25 j＝60 k＝65
i＝27 j＝36 k＝45
i＝28 j＝45 k＝53
i＝30 j＝40 k＝50
i＝30 j＝72 k＝78
i＝32 j＝60 k＝68
i＝33 j＝44 k＝55
i＝33 j＝56 k＝65
i＝35 j＝84 k＝91
i＝36 j＝48 k＝60
i＝36 j＝77 k＝85
i＝39 j＝52 k＝65
i＝39 j＝80 k＝89
i＝40 j＝42 k＝58
i＝40 j＝75 k＝85
i＝42 j＝56 k＝70
i＝45 j＝60 k＝75
i＝48 j＝55 k＝73
i＝48 j＝64 k＝80
i＝51 j＝68 k＝85
i＝54 j＝72 k＝90
i＝57 j＝76 k＝95
i＝60 j＝63 k＝87
i＝65 j＝72 k＝97
……………………
……………………
2：如图，A、B两个小集镇在河流CD的同侧，分别到河的距离为AC=10千米，BD=30千米，且CD=30千米，现在要在河边建一自来水厂，向A、B两镇供水，铺设水管的费用为每千米3万，请你在河流CD上选择
知识要点归纳：
30 40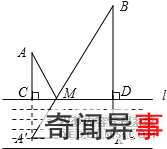
作A关于CD的对称点A′，连接A′B与CD，交点为M，点M即为所求作的点．
则可得：DK=A′C=AC=10千米，
∴BK=BD+DK=40千米，
∴AM+BM=A′B=
总费用为50×3=150万元．
3：好的勾股定理练习题
知识要点归纳：
勾股定理单元检测
1．选择题（每小题2分,共20分）
（1）等腰直角三角形三边的平方比为（）
A．1：4：1
B．1：2：1
C．1：8：1
D．1：3：1
（2）下列三角形中,是直角三角形的是（）
A．三角形的三边满足a+b=2c
B．三角形三边的平方比为3：4：5
C．三角形的一边等于另一边的一半
D．三角形的三边为9,40,41
（3）小明家与学校的距离仅有500m,但需要拐一个直角弯才能到达,已知拐弯处到学校有400m,则家门口到拐弯处有（）
A．300m
B．350m
C．400m
D．450m
（4）有一个木工师傅测量了等腰三角形的腰、底边和高的长,但他把这三个数据与其他数据弄混了,请你帮他找出来（）
A．13,12,12
B．12,12,8
C．13,10,12
D．5,8,4
（5）△ABC中,∠C=90°,a+c=32,a：c=3：5,则△ABC的周长为（）
A．30
B．40
C．48
D．50
（6）将直角三角形的各边扩大相同的倍数,得到的三角形是（）
A．锐角三角形
B．直角三角形
C．钝角三角形
D．无法确定
（7）正方形的对角线长是18,则这个正方形的面积是 （ ）
A．9
B．18
C．162
D．81
（8）在△ABC中,AB=13,AC=15,高AD=12,则BC的长是 （ ）
A．14
B．9
C．9或5
D．4或14
（9）若a、b、c为△ABC的三边长,且满足a2+ab－ac－bc=0,b2+bc－ba－ca=0,则△ABC的形状是 （ ）
A．直角三角形
B．等腰三角形
C．等腰直角三角形
D．等边三角形
（10）设a、b都是正整数,且a－b,3b,a+b （a＞2b）构成一个直角三角形三边的长,则这个三角形的任一边的长不可能是 （ ）
A．12
B．13
C．14
D．15
2．填空题（每小题2分,共20分）
（11）三角形中两边的平方差恰好等于第三边的平方,则这个三角形是 三角形．
（12）在Rt△ABC中,∠C=90°,c=20,b=12,则a= .
（13）在△ABC中,a=3,b=7,c2=58,则S△ABC= .
（14）在Rt△ABC中,∠C=90°,c=20,a：b=3：4,则a= ,b= .
（15）在Rt△ABC中,直角边AC=5,BC=12,则斜边AB上的高等于 .
（16）已知Rt△ABC的三边长是三个连续整数,则这个三角形的斜边长为 .
（17）在长、宽、高分别为l dm、2dm、2dm的长方体箱子内能放入的最长物体的长度是 dm．
（18）某车间的人字形屋架呈等腰三角形,跨度AB=24 m,上弦AC=13 m,则中柱CD（D为AB的中点）的长为 m．
（19）要登上12m高的建筑物,为了安全起见,需使梯子底端离建筑物5m,则至少需要 m的梯子．
（20）Rt△ABC的三边长从大到小排列为m、n、13,且m、n都是正整数,则△ABC的周长为 .
3．解答题（每小题12分,共60分）
（21）在△ABC中,AD⊥BC于点D,AB=25,AC=30,AD=24,试判断△ABC的形状．
勾股定理单元检测
1．选择题（每小题2分,共20分）
（1）等腰直角三角形三边的平方比为（）
A．1：4：1
B．1：2：1
C．1：8：1
D．1：3：1
（2）下列三角形中,是直角三角形的是（）
A．三角形的三边满足a+b=2c
B．三角形三边的平方比为3：4：5
C．三角形的一边等于另一边的一半
D．三角形的三边为9,40,41
（3）小明家与学校的距离仅有500m,但需要拐一个直角弯才能到达,已知拐弯处到学校有400m,则家门口到拐弯处有（）
A．300m
B．350m
C．400m
D．450m
（4）有一个木工师傅测量了等腰三角形的腰、底边和高的长,但他把这三个数据与其他数据弄混了,请你帮他找出来（）
A．13,12,12
B．12,12,8
C．13,10,12
D．5,8,4
（5）△ABC中,∠C=90°,a+c=32,a：c=3：5,则△ABC的周长为（）
A．30
B．40
C．48
D．50
（6）将直角三角形的各边扩大相同的倍数,得到的三角形是（）
A．锐角三角形
B．直角三角形
C．钝角三角形
D．无法确定
（7）正方形的对角线长是18,则这个正方形的面积是 （ ）
A．9
B．18
C．162
D．81
（8）在△ABC中,AB=13,AC=15,高AD=12,则BC的长是 （ ）
A．14
B．9
C．9或5
D．4或14
（9）若a、b、c为△ABC的三边长,且满足a2+ab－ac－bc=0,b2+bc－ba－ca=0,则△ABC的形状是 （ ）
A．直角三角形
B．等腰三角形
C．等腰直角三角形
D．等边三角形
（10）设a、b都是正整数,且a－b,3b,a+b （a＞2b）构成一个直角三角形三边的长,则这个三角形的任一边的长不可能是 （ ）
A．12
B．13
C．14
D．15
2．填空题（每小题2分,共20分）
（11）三角形中两边的平方差恰好等于第三边的平方,则这个三角形是 三角形．
（12）在Rt△ABC中,∠C=90°,c=20,b=12,则a= .
（13）在△ABC中,a=3,b=7,c2=58,则S△ABC= .
（14）在Rt△ABC中,∠C=90°,c=20,a：b=3：4,则a= ,b= .
（15）在Rt△ABC中,直角边AC=5,BC=12,则斜边AB上的高等于 .
（16）已知Rt△ABC的三边长是三个连续整数,则这个三角形的斜边长为 .
（17）在长、宽、高分别为l dm、2dm、2dm的长方体箱子内能放入的最长物体的长度是 dm．
（18）某车间的人字形屋架呈等腰三角形,跨度AB=24 m,上弦AC=13 m,则中柱CD（D为AB的中点）的长为 m．
（19）要登上12m高的建筑物,为了安全起见,需使梯子底端离建筑物5m,则至少需要 m的梯子．
（20）Rt△ABC的三边长从大到小排列为m、n、13,且m、n都是正整数,则△ABC的周长为 .
3．解答题（共60分）
（21）在△ABC中,AD⊥BC于点D,AB=25,AC=30,AD=24,试判断△ABC的形状．
已知a、b、c为△ABC的三边,且满足a2c2－b2c2=a4－b4,试判断△ABC的形状．
因为a2c2－b2c2=a4－b4,
所以c2（a2－b2）=（a2－b2）（a2+b2）．
所以c2=a2+b2．
所以△ABC是直角三角形．
回答下列问题：
（ⅰ）上述解题过程,从哪一步开始出现错误?请写出该步代码为 ；
（ⅱ）错误的原因为 ；
（ⅲ）请你将正确的解答过程写下来．
答案
1．（1）B
（2）D
（3）A
（4）C
（5）C
（6）B
（7）C
（8）D
（9）D
（10）C
2．（11）直角
（12）16
（13）10．5
（14）12 16
（15）
（16）5
（17）3
（18）5
（19）13
（20）182
3．（21）在Rt△ABD中,BD2=252－242=49,
所以BD=7,同理CD=18．
所以BC=25．所以△ABC是等腰三角形．
4：勾股定理习题一根竹子,原来高一丈,虫子伤有病,一阵风把竹子折断,竹梢恰好到地面上,抵地处离原长的竹子3尺远处,问原处还有多高的竹子?一个2.5米长的梯子靠在一座建筑物上,梯子的底部离
知识要点归纳：
1.
1丈 = 10 尺
你应该理解题意吧?
由图看出现在剩下的那一部分竹子,地面(3尺)和折断的竹子组成了一个直角三角形.其中 剩下的那一部分竹子和地面(3尺)是直角边,折断的竹子是斜边.
于是根据勾股定理就可以列出方程了.
设现在剩下的那一部分竹子为x,折断的竹子的长度就是(10-x)尺.
x^2+3^2=(10-x)^2
x^2+9=x^2-20x+100
20x=91
x=4.55
所以原处还有4.55尺竹子.
2.
在题目中,梯子的长度是永远不变的.梯子,建筑物,地面组成了一个直角三角形.
我们首先求出原来梯子的顶部离建筑物底部的距离,从而根据勾股定理求出梯子下滑后顶部离建筑物底部的距离（减去0.4）,再求出移动后梯子的底部离建筑物的距离（勾股定理）,最后就可以求出梯子向外移动了多少了.
原来梯子的顶部离建筑物底部的距离：√(2.5^2-0.7^2)=2.4（米）
梯子下滑后顶部离建筑物底部的距离：2.4-0.4=2（米）
移动后梯子的底部离建筑物的距离：√(2.5^2-2^2）=1.5（米）
梯子向外移动了：1.5-0.7=0.8（米）
5：【数学勾股定理练习题!求答案!急!在四边形ABCD中,AC⊥BD与O,是否有AB的平方+CD的平方=AD的平方+BC的平方?【我想这个四边形应该是正方形,可是不知用什么语言去证明】（请各位帮我写出证明过程】
知识要点归纳：
因为 AC⊥BD与O,AC BD分别是四边形ABCD的对角线,所以有：
三角形 AOB DOC BOC AOD都是直角三角形,既有：
AB平方=OA平方+OB平方
CD平方=OD平方+OC平方
BC平方=OB平方+OC平方
AD平方=AO平方+OD平方
所以有 AB平方+DC平方=BC平方+AD平方.
这个四边形不一定是正方形.只要满足两条对角线相互垂直的四边形,它的四条边都有这个关系.
猜你喜欢：
1：初二数学勾股定理难一点的应用题，要有答案。谢谢。
提示：23．求下列各式中x的值． （1）16x2﹣81=0； （2）﹣（x﹣2）3﹣64=0． 24．设2+的整数部分和小数部分分别是x、y，试求x、y的值与x﹣1的算术平方根． 25．将一个体积为216cm3的正方体分成等大的8个小正方体，求每个小正方体的表面积． 26．如图...
2：勾股定理练习题
提示：北师版八年级上册,题目综合性稍微强一些,但都是勾股定理的基本应用。 http://wenku.baidu.com/view/c1b3c203bed5b9f3f90f1ca9.html
3：谁能帮我出一道关于勾股定理的题？
提示：．等边三角形的高是h，则它的面积是( ) A． h2B． h2C． h2D． h2 答案：B 说明：如图，ΔABC为等边三角形，AD⊥BC，且AD=h，因为∠B=60º，AD⊥BC，所以∠BAD=30º；设BD=x，则AB=2x，且有x2+h2=(2x)2，解之得x= h，因为BC=2BD= h，所以SΔAB...
4：勾股定理很难的题？（最好有答案）谢谢了，大神帮忙啊
提示：迷惑题 (1)有3个人去投宿, 一晚30元. 三个人每人掏了10元凑够30元交给了老板. 后来老板说今天优惠只要25元就够了, 拿出5元命令服务生退还给他们, 服务生偷偷藏起了2元, 然后, 把剩下的3元钱分给了那三个人, 每人分到1元. 这样, 一开始每人掏了10...
5：我需要最最最基础的勾股定理题
提示：1、在Rt△ABC中，∠C=90°，三边长分别为a、b、c，则下列结论中恒成立的是（ ） A、2abc2 D、2ab≤c2 2、已知x、y为正数，且│x2-4│+（y2-3）2=0，如果以x、y的长为直角边作一个直角三角形，那么以这个直角三角形的斜边为边长的正方形的面积为（ ） A...
