知识点：《二次函数的应用》 收集：宦下逗 编辑：栀子花女孩
本知识点包括：1、二次函数的应用 2、二次函数的应用题怎么解？技巧。 3、二次函数可以应用在生活中的什么方面？ 4、二次函数的应用性质 5、二次函数的应用 调查报告 。
《二次函数的应用》相关知识
函数应用题的解题技巧是贴进社会生产和生活实际的数学应用问题,充分体现了数学基本方法的灵活运用和基本数学思想的渗透.下面就函数应用题的类型及解法举例分析.
一． 函数模型为反比例函数问题
例1：学校请了30个木匠,要制作200把椅子和100张课桌.已知制作一张课桌与一把椅子的工时之比为10：7,问30个木匠应当如何分组（一组制课桌另一组制椅子）,能使完成全部任务最快?
分析：对于本题要注意用变化的观点分析和探求具体问题中的数量关系,寻找已知量与未知量之间的内在联系,然后将这些内在联系与数学知识联想,建立函数关系式或列出方程,利用函数性质或方程的观点去解,使应用问题化生为熟,尽快得到解决.
设x个木匠制课桌,（30-x）个木匠制椅子,一个木匠在一个单位时间里可制7张课桌或10把椅子,所以制作100张课桌所需时间为函数,制作200把椅子所需时间为函数 ,完成全部任务所需时间为函数y（x）=max{P（x）,Q（x）}
要求的y（x）的最小值,需满足P（x）=Q（x）,即 解得x=12.5 , 考虑到人数为整数,考查P（12）与Q（13）, P（12）=
Q（13）= 即y（12）>y（13）,
所以用13个木匠制课桌,17个木匠制椅子完成全部任务最快.
二．函数模型为一次函数问题
例2：某家报刊买进报纸的价格是每份0.35元,卖出的价格是每份0.50元,卖不掉的报纸还可以每份0.80元的价格退回报社.在一个月(30天)里,又20天每天可以卖出400份,其余10天每天只能卖出250份.设每天从报社买进的报纸的数量相同,则应该每天从报社卖劲多少份,才能使每月所获的利润最大?并计算该销售点一个月最多可赚得多少元?
分析：此题主要在于分析题目中的条件,建立合适的关系式,应用函数的性质去解决问题,并考虑在定义域内的局限性与实际意义.如此题每月所赚的钱=卖报所得的金额—付给报社的金额.而卖报所得的金额分三部分.从而可列出函数解析式.
设每天应从报社买x份,可的250≦x≦400,设每月赚y元,得
y=0.5x·20+0.5×250×10+（x-250）×0.08×10-0.35·x·30
=0.3x+1050 x∈[250,400]
因为y =0.3x+1050是定义域上的增函数,所以当x=400时, y大=120+1050=1170（元)
答：每天从报社卖进400份, 使每月所获的利润最大,每月可赚得1070元.
三．函数模型为一二次函数问题
例3：有（m）长的钢材,要做成如图所示的窗架,上半部分为半圆,下半部分为六个全等矩形组成的矩形,试问小矩形的长宽比为多少时,窗所通过的光线最多,并算出窗框的最大值.
分析：应用数学知识解决应用型问题,是提高数学素质的训练内容之一,教材中也多出出现,对于此题的分析要注意观察问题的结构特征,揭示内在联系,挖掘隐含条件,从而恰当的构造出函数,应用函数的具体性质去解决问题.本题中面积为两部分够成,而面积就为窗所通过的光线,从而可列出函数解析式进一步解出题目.
设小矩形的长为x, 宽y为 ,则由图形可得：
11x+x+9y= ∴9y=-(11+)x
要使窗所通过的光线最多,即要窗框的面积最大,则
S==+[x-(11+)x2]
=-(x-+.
所以当x= , y=
即=1：1 此时窗框的面积s有最大值S=
四．函数模型为其他函数问题
例4：有甲乙两种商品,销售这两种商品所获得的利润依次是P和Q（万元）,他们与投入资金Q（万元）的关系,有经验公式： 今有3万元资金投入销售甲乙两种商品,为获得的利润最大,对甲乙两种商品的资金投入分别应为多少?能获得最大的利润是多少?
分析：首先应根据题意,建立利润与资金之间的函数关系,求的函数解析式,然后再转化为求函数的最大值问题.求解本题的关键是建立目标函数及求最值的方法,换元法是求无理函数最值的常用方法,在换元过程中要注意变量的取值范围的变化.
设对甲种商品投资x万元,则乙种商品投资（3-x）万元,总利润y万元,据题意有：
Y= （ 0≦x≦3 ）
设=t 则x=3-t2, 0≦x≦
所以 y= 0≦x≦
当x=时 y大=1.05, 此时x=0.75 ,3-x=2.25
由此可知,为获得最大利润,对甲乙两种商品的资金投入应分别为0.75万元和2.25万元, 获的总利润为1.05万元
总之,函数的应用是数学思想的体现,是应用数学知识解决实际问题的有效途经.如果我们学好了这部分,在具体的题目中会分析题目,找出关系量之间的联系,建立适当的函数关系式,把实际问题转化为数学模型,然后利用初等函数的性质,去解决问题.使抽象问题数学化,化生为熟.
知识拓展：
1：【某商场在销售旺季临近时，某品牌的童装销售价格呈上升趋势，假如这种童装开始时的售价为每件20元，并且每周（7天）涨价2元，从第6周开始，保持每件30元的稳定价格销售，直到11周结束】
知识要点归纳：
（1）y=20+2(x?1)＝2x+18(1≤x＜6) 30(6≤x≤11)
（2）设利润为W，则
W=
|
W=
| 1 |
| 8 |
∴当x=5时，W最大=
| 25 |
| 8 |
W=
| 1 |
| 8 |
∴当x=11时，W最大=
| 1 |
| 8 |
| 1 |
| 8 |
综上可知：在第11周进货并售出后，所获利润最大且为每件19.125元．
2：初三二次函数应用题1.抛物线y=(k^2-2)x^2+m-4kx的对称轴是直线x=2,且最低点在y=-1/2x+2上,求该二次函数的关系式2.已知抛物线y=x^2-(k+3)x+2k-1.设抛物线与x轴交与A、B两点,（A在左边）顶点为C,C点的纵
知识要点归纳：
1.抛物线y=(k²-2)x²+m-4kx的对称轴是直线x=2,且最低点在y=-1/2x+2上,求该二次函数的关系式
抛物线y=(k²-2)x²+m-4kx的对称轴方程x=-b/(2a)=4k/[2(k²-2)]=2,故：k=2或k=-1
当k=2时,抛物线y=(k²-2)x²+m-4kx简化为：y=2x²-8x+m=2(x-2) ²+m-8,最低点坐标为（2,m-8）在y=-1/2x+2上,即：m-8=-1/2×2+2,故：m=9,故：该二次函数的关系式为：y=2x²-8x+9
当k=-1时,k²-2＝－1＜0,没有最低点,故舍去
故：该二次函数的关系式为：y=2x²-8x+9
2.已知抛物线y=x²-(k+3)x+2k-1.设抛物线与x轴交与A、B两点,（A在左边）顶点为C,C点的纵坐标为m,求（AB）²/m的值
设A（x1,0）、B(x2,0)
故：x1+x2= k+3,x1•x2=2k-1
故：（AB）²＝（x1-x2）²=(x1+x2) ²-4 x1•x2=k²-2k+13
又：顶点纵坐标m=(4ac-b²)/(4a)=[4(2k-1)-( k+3) ²]/4=-( k²-2k+13)/4
故：（AB）²/m= (k²-2k+13)÷[-( k²-2k+13)/4]=-4
3：二次函数利润应用题利达经销店为某工厂代销一种建筑材料,当每吨售价为260元时,月销售量为45吨,该经销售店为提高经营利润,准备采取降价的方式进行促销,经市场调查发现：当每吨售价每下
知识要点归纳：
（1）当售价为240元时,此时的月销量为（260-240）/10X7.5+45=60吨
（2）y与x的函数关系式为x[(260-x)/10X7.5+45]-100[(260-x)/10X7.5+45]=y
即为（x-100）[(260-x)/10X7.5+45]=y
（3）该经销店要获得最大月利润,售价应定为每吨210元,此时的利润为9075元.
（4）“当月利润最大时,月销售额也最大”不对,由（3）的结论知道利润最大为每吨210元时此时的月销售额为（260-210）/10X7.5+45=82.5吨.但是当售价额是由式（260-x）/10X7.5+45求出的,由此可知随着售价的降低销售额就会随之提高,所以小静的说法不对
4：已知抛物线y=-x2+2（k-1）x+k+2与x轴交于A、B两点，且点A在x轴的负半轴上，点B在x轴的正半轴上．（1）求实数k的取值范围；（2）设OA、OB的长分别为a、b，且a：b=1：5，求抛物线的解析式；（3）
知识要点归纳：
x x x x a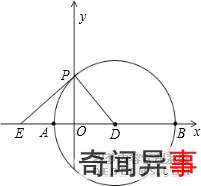
（1）设点A（x1，0），B（x2，0）且满足x1＜0＜x2
由题意可知x1x2=-（k+2）＜0，即k＞-2．
（2）∵a：b=1：5，设OA=a，即-x1=a．
则OB=5a，即x2=5a，a＞0
∴
|
∴k=2a+1，
即5a2-2a-3=0，解得a1=1，
a
2＝?| 3 |
| 5 |
∴k=3
∴抛物线的解析式为y=-x2+4x+5．
（3）由（2）可知，当-x2+4x+5=0时，可得x1=-1，x2=5．
即A（-1，0），B（5，0），
∴AB=6，则点D的坐标为（2，0）
当PE是⊙D的切线时，PE⊥PD
由Rt△DPO∽Rt△DEP可得PD2=OD?DE
即32=2×DE
∴DE=
| 9 |
| 2 |
| 9 |
| 2 |
| 5 |
| 2 |
故点E的坐标为（-
| 5 |
| 2 |
5：二次函数应用题随便来一个
知识要点归纳：
二次函数应用题训练专项中考类型(三)
(二).建模题
1．某食品零售店为仪器厂代销一种面包,未售出的面包可退回厂家,经统计销售情况发现,当这种面包的单价定为7角时,每天卖出160个.在此基础上,这种面包的单价每提高1角时,该零售店每天就会少卖出20个.考虑了所有因素后该零售店每个面包的成本是5角.设这种面包的单价为x（角）,零售店每天销售这种面包所获得的利润为y（角）.
⑴用含x的代数式分别表示出每个面包的利润与卖出的面包个数；
⑵求y与x之间的函数关系式；⑶当面包单价定为多少时,该零售店每天销售这种面包获得的利润最大?最大利润为多少?
2．某工厂生产的某种产品按质量分为个档次,生产第一档次（即最低档次）的产品一天生产件,每件利润元,每提高一个档次,利润每件增加元．
每件利润为元时,此产品质量在第几档次?
由于生产工序不同,此产品每提高一个档次,一天产量减少件．若生产第档的产品一天的总利润为元（其中为正整数,且≤≤）,求出关于的函数关系式；若生产某档次产品一天的总利润为元,该工厂生产的是第几档次的产品?
3．某机械租赁公司有同一型号的机械设备40套.经过一段时间的经营发现：当每套机械设备的月租金为270元时,恰好全部租出.在此基础上,当每套设备的月租金每提高10元时,这种设备就少租出一套,且没租出的一套设备每月需支出费用（维护费、管理费等）20元.设每套设备的月租金为x（元）,租赁公司出租该型号设备的月收益（收益＝租金收入－支出费用）为y（元）.
用含x的代数式表示未出租的设备数（套）以及所有未出租设备（套）的支出费
求y与x之间的二次函数关系式；
当月租金分别为300元和350元式,租赁公司的月收益分别是多少元?此时应该出租多少套机械设备?请你简要说明理由；
请把（2）中所求出的二次函数配方成的形式,并据此说明：当x为何值时,租赁公司出租该型号设备的月收益最大?最大月收益是多少?
4．某商店购进一批单价为18元的商品,如果以单价20元出售,那么一个星期可售出100件.根据销售经验,提高销售单价会导致销售量减少,即当销售单价每提高1元,销售量相应减少10件,如何提高销售单价,才能在一个星期内获得最大利润?最大利润是多少?
5．某市城建部门经过长期市场调查发现,该市年新建商品房面积P(万平方米)与市场新房均价x(千元/平方米)存在函数关系P=25x；年新房销售面积Q(万平方米)与市场新房均价x(千元/平方米)的函数关系为Q=―10；
如年新建商品房的面积与年新房销售面积相等,求市场新房均价和年新房销售总额；
在(1)的基础上,如果市场新房均价上涨1千元,那么该市年新房销售总额是增加还是减少?变化了多少?结合年新房销售总额和积压面积的变化情况,请你提出一条合理化的建议.(字数不超过50)
6.在黄州服装批发市场,某种品牌的时装当季节将来临时,价格呈上升趋势,设这种时装开始时定价为20元,并且每周（7天）涨价2元,从第6周开始保持30元的价格平稳销售；从第12周开始,当季节即将过去时,平均每周减价2元,直到第16周周末,该服装不再销售.
⑴试建立销售价与周次之间的函数关系式；⑵若这种时装每件进价Z与周次次之间的关系为Z＝.1≤≤16,且为整数,试问该服装第几周出售时,每件销售利润最大?最大利润为多少?
7. 某食品批发部准备用10000元从厂家购进一批出厂价分别为16元和20元的甲、乙两种酸奶,然后将甲、乙两种酸奶分别加价20％和25％向外销售.如果设购进甲种酸奶为x(箱),全部售出这批酸奶所获销售利润为y(元).
求所获销售利润y(元)与x(箱)之间的函数关系式；
根据市场调查,甲、乙两种酸奶在保质期内销售量都不超过300箱,那么食品批发部怎样进货获利最大,最大销售利润是多少?
8.某企业在“蜀南竹海”收购毛竹进行粗加工,每天可加工8吨,每吨可获利800元；如果对毛竹进行精加工,每天可加工1吨,每吨可获利4000元.由于受条件限制,每天只能采用一种方式加工,要求在一月内（30天）将这批毛竹全部销售.为此企业厂长召集职工开会,让职工讨论如何加工销售更合算? 甲说：将毛竹全部进行粗加工后销售； 乙说：30天都进行精加工,未加工的毛竹直接销售； 丙说：30天中可用几天粗加工,再用几天精加工后销售；请问厂长应采用哪位说的方案做,获利最大?
9. 某公园出售的一次性使用门票,每张10元,同时又推出购买“个人年票”的售票方法（从购买日起,可供持票者使用一年）,年票分A、B两类：A类年票每张100元,持票者每次进入公园无需再购买门票,；B类年票每张40元,持票者每次进入公园时需再购买每次2元的门票.现有甲、乙、丙三位游客在一年中分别选择用A类年票、B类年票、一次性使用门票三种方式去游园,并且乙、丙每人一年中恰好都进入该公园x次.
⑴请分别写出乙、丙每人一年的门票费支出（用含x的代数式表示）
⑵在三位游客每人一年的门票费支出中,当甲的支出为最少时：①问乙、丙每人一年中进入该公园至少超过多少次?②求此时三位游客一年中游园共支出的门票费总额的最小值.
10. 在黄州服装批发市场,某种品牌的时装当季节将来临时,价格呈上升趋势,设这种时装开始时定价为20元,并且每周（7天）涨价2元,从第6周开始保持30元的价格平稳销售；从第12周开始,当季节即将过去时,平均每周减价2元,直到第16周周末,该服装不再销售.
⑴试建立销售价与周次之间的函数关系式；
⑵若这种时装每件进价Z与周次次之间的关系为Z＝.1≤≤16,且为整数,试问该服装第几周出售时,每件销售利润最大?最大利润为多少?
11．某市今年来经济发展速度很快,根据统计：该市国内生产总值1990年为8.6亿元人民币,1995年为10.4亿元人民币. 经论证,上述数据适合一个二次函数关系.请根据这个函数关系,预测2005年该市国内生产总值将达到多少?
猜你喜欢：
1：二次函数的应用
提示：一般地，自变量x和因变量y之间存在如下关系： 一般式：1：y=ax^2;+bx+c(a≠0，a、b、c为常数)， 则称y为x的二次函数。顶点坐标(-b/2a,(4ac-b^2)/4a) (若给出抛物线上两点及另一个条件，通常可设一般式） 2：顶点式：y=a(x-h）^2+k或y=a(x+m)^2+k ...
2：二次函数的应用题怎么解？技巧。
提示：对于二次函数，一次函数，反比例函数都要有技巧，主要是；首先弄清它们的表达式及字母表示然后记住k的取值是大于还是小于0，还有就是a,b,c的取值，在二次函数当中主要记住二次函数的图象：二次函数y=ax2＋bx＋c的图象是一条抛物线二次函数的三种...
3：二次函数可以应用在生活中的什么方面？
提示：可以与物理相结合，利用S=0.5*gt2（0.5乘以重力加速度乘以时间的平方）计算物体下落路程。 在企业其利润随投资的变化关系一般可用二次函数表示。 例题如下 一汽车出租公司拥有汽车100辆，当每辆车的月租金为3000元时，可全租出。当每辆车月租金...
4：二次函数的应用性质
提示：函数性质编辑 1.二次函数是抛物线，但抛物线不一定是二次函数。开口向上或者向下的抛物线才是二次函数。抛物线是轴对称图形。对称轴为直线 。[3] 对称轴与抛物线唯一的交点为抛物线的顶点P。特别地，当b=0时，抛物线的对称轴是y轴（即直线x=0）...
5：二次函数的应用 调查报告
提示：二次函数（quadratic function）是指未知数的最高次数为二次的多项式函数。二次函数可以表示为f(x)=ax^2+bx+c(a不为0)。其图像是一条主轴平行于y轴的抛物线。 义与定义表达式 一般的，自变量x和因变量y之间存在如下关系： 一般式 y=ax^2+bx+c(a≠...
