知识点：《余璇》 收集：扈倨沿 编辑：栀子花女孩
本知识点包括：1、边长为5、7、8的三角形的最大角与最小角之和是多少 2、爱干净的妈妈 作文400字 3、第四题 已知cos阿尔法等于五分之三，cos(阿尔法加... 4、复变函数题，，求f(t)=sintcost的傅里叶变换 5、泰国迎来买房黄金时代? 。
《余璇》相关知识
容易,但现在没时间了,我会尽快把答案告诉你
不好意思,这几天太忙了,现在告诉你啊
可以设CF=X,大正方形边长等于a,小正方形边长等于b,那么就有AG的平方等于（a+b）的平方+（a-b）的平方,AF的平方等于a的平方+x的平方,FG的平方等于b的平方+（a+b-x）的平方,由余弦定理可知：
二分之根号二=（AG的平方+AF的平方-FG的平方）/2AG*AF
代入并整理得：b(x的平方）+（a的平方-b的平方）X-a的平方b=0
解得:x=-a/b 或 x=b,显然X应该是正值,那么X应该等于b,
所以AC=FE=a,CF=GE=b,所以三角形ACF与三角形FEG全等,那么就会有AF=FG,所以角AGF=45度,所以角AFG=90度,所以三角形AFG为等腰直角三角形.
知识拓展：
1：【如图，在菱形ABCD中，∠B=60°，点E、F分别从点B、D出发以同样的速度沿边BC、DC向点C运动．给出以下四个结论：①AE=AF；②∠CEF=∠CFE；③当点E，F分别为边BC，DC的中点时，△AEF是等边三角形；】
知识要点归纳：
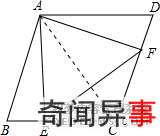∵点E、F分别从点B、D出发以同样的速度沿边BC、DC向点C运动，
∴BE=DF，
∵AB=AD，∠B=∠D，
∴△ABE≌△ADF，
∴AE=AF，①正确；
∴CE=CF，
∴∠CEF=∠CFE，②正确；
∵在菱形ABCD中，∠B=60°，
∴AB=BC，
∴△ABC是等边三角形，
∴当点E，F分别为边BC，DC的中点时，BE=1 2
| 1 |
| 2 |
∴△ABE和△ADF是直角三角形，且∠BAE=∠DAF=30°，
∴∠EAF=120°-30°-30°=60°，
∴△AEF是等边三角形，③正确；
∵△AEF的面积=菱形ABCD的面积-△ABE的面积-△ADF的面积-△CEF的面积=
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
| ||
| 4 |
∴△AEF的面积是BE的二次函数，
∴当BE=0时，△AEF的面积最大，④错误．
故正确的序号有①②③．
2：..在直角三角形ABC中,D、E、F分别是三边上的任意点,已知直角三角形三边分别为3、4、5,请问三角形DEF周长的最小值是多少?（要具体过程.）
知识要点归纳：
在一个三角形ABC中,有一个内三角形PDE.AB是底边,点P在AB边上,点D在AC边上,点E在BC边上.在某个特殊的位置上,三角形PDE有一个最小值周长.
求：当三角形PDE的周长是最小值时,点P处于AB边上一个特殊的位置.点P在哪里?点D和点E又在哪里?最小值周长是多少?
根据提示,连接CP、CR、CT,设PR交AC于H,PT交BC于H'
显然,D、E只有分别对应RT与AC、BC的交点,三角形DEP的周长才是最小的,也就是此时三角形DEF的周长就是RT的长度
因为RH＝PH,且角CH垂直于RP,所以三角形RCH与三角形PCH全等,
故有角RCH＝角PCH,CR＝CP
同理可证角TCH'=角PCH',CT＝CP
所以CR＝CP＝CT
所以角RCT＝2倍角ACB
由余弦定理RT^2=CR^2+CT^2-2*CR*CT*cos角RCT
又根据上面得出的结论,用CP分别替代CR、CT,用2倍角ACB替代角RCT
有RT^2=2*CP^2*(1-cos2倍角ACB)
因为角ACB为定值,显然,只有当CP最小时,RT才是最小的
所以P点为从C作垂线与AB的交点,D、E两点就是RT与AC、BC的交点(也可以证明这两点也是垂线的交点）
要求最小周长,得把CP用三角形的边和角表示出来,可有多种选择
我用CP＝AC*sin角CAB表示
则RT^2=2*(AC*sin角CAB)^2*(1-cos2倍角ACB)
开方后即得内接三角形周长的最小值
注：RT^2表示RT的平方的意思,其它的类推
3：如图，在等腰Rt△ABC中，∠A=90°，AC=9，点O在AC上，且AO=2，点P是AB上一动点，连接OP将线段OP绕O逆时针旋转90°得到线段OD，要使点D恰好落在BC上，则AP的长度等于______．
知识要点归纳：
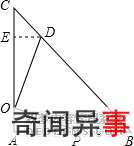过点D作DE⊥AC于E，
则∠DOE+∠AOP=90°，∠DOE+∠ODE=90°，
∴∠ODE=∠AOP，
又∵OD=OP，∠DEO=∠OAP=90°，
∴△DEO≌△OAP，
∴DE=OA=CE=2，
∴AP=OE=9-4=5．
故答案为：5．
4：在三角形ABC中,角B=2倍的角A,AD平分角BAC,求证AC=AB+BD,图,
知识要点归纳：
在ab延长线上截取BN=BD连接ND
所以∠N=∠BDN
因为∠ABD=2∠BAC
所以∠N=∠BDN =∠BAC
因为AD平分∠BAC
所以∠BAD=∠CAD=1/2∠BAC
根据外角等于与之不相邻的两内角和
所以∠ADC=5/2∠BAC
根据三角形内角和
∠C=∠BAC
又因为AD为公共边
所以三角形NAD和三角形CAD全等
所以AN=AC
所以AB+BN=AC
即AB+BD=AC
5：一道初中数学平面几何题如图,锐角三角形ABC内接于圆O,H为三角形ABC的垂心,OD垂直BC,垂足为D.求证：OD=1/2AH
知识要点归纳：
作OE⊥AB,垂足为E； EF//AH,交BH于F
很明显,E为AB的中点；F为BH的中点,故EF=1/2AH
又 D为BC的中点；F为BH的中点,故 FD//HC
因为 HC⊥AB； OE⊥AB,
所以 OE//CH//FD
故 EFOD为平行四边形
所以 OD=EF=1/2AH
猜你喜欢：
1：边长为5、7、8的三角形的最大角与最小角之和是多少
提示：用余弦公式 解:设三角形ABC中 a=5 b=7 c=8 则锐角三角形中最大角与最小角为C和A b方=a方+c方-2ac*cosB 解得cosB=1/2 B=60度 A+C=...
2：爱干净的妈妈 作文400字
提示：我有一个爱整洁的妈妈,爱整洁,这既是她的优点,也是缺点。让我先来讲讲吧! 每当妈妈下班回家,都会把家里收拾的井井有序,每个东西从哪里拿的就放必须...
3：第四题 已知cos阿尔法等于五分之三，cos(阿尔法加...
提示：第四题已知cos阿尔法等于五分之三,cos(阿尔法加贝塔)等于负五分之三求cos贝塔第五题sin80°-√3cos80°...
4：复变函数题，，求f(t)=sintcost的傅里叶变换
提示：sintcost=1/2sin2t F(1/2sin2t) =∫(-∞,+∞) 1/2sin2t · e^-jwt dt 用欧拉公式可得原式= 1/2∫(-∞,+∞) j/2( e^-2jt - e...
5：泰国迎来买房黄金时代?
提示：泰国,“一带一路”最大受益国,中泰铁路已经开工建设了
